计算几何的本质就是背板 ——卢爷

特此鸣谢为我们讲课/布置作业的LJZ学长

基础技能

输出时的精度控制

输出前要加上eps（有的时候除法会造成浮点数末尾是一串连续的9的情况）
POJ这种毒瘤OJ，输出double的格式控制符是%f

下面介绍一下标准输入输出流输出浮点数的方法：

#include <iostream>
#include <iomanip>
using namespace std;

int main()
{
    const double value = 12.3456789;

    cout << value << endl; // 默认以6精度，所以输出为 12.3457
    cout << setprecision(4) << value << endl; // 改成4精度，所以输出为12.35
    cout << setprecision(8) << value << endl; // 改成8精度，所以输出为12.345679
    cout << fixed << setprecision(4) << value << endl; // 加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位，输出为12.3457
    cout << value << endl; // fixed和setprecision的作用还在，依然显示12.3457
    cout.unsetf( ios::fixed ); // 去掉了fixed，所以精度恢复成整个数值的有效位数，显示为12.35
    cout << value << endl;
    cout.precision( 6 ); // 恢复成原来的样子，输出为12.3457
    cout << value << endl;
}

更详细的信息参见：C++ 标准输出控制小数点后位数的方法和C++ 标准输出如何控制小数点后位数

叉积和点积

这里是向量运算模块的代码：

struct Point {
	double x, y;
	Point(double x=0,double y=0){}
	friend Point operator + (const Point &a, const Point &b) {return Point(a.x + b.x, a.y + b.y);}
	friend Point operator - (const Point &a, const Point &b) {return Point(a.x - b.x, a.y - b.y);}
	friend Point operator * (const Point &a, const double &b) {return Point(a.x * b, a.y * b);}
	double norm() {return sqr(x) + sqr(y);}
} p[maxn];
double det(Point a, Point b) {
    return a.x * b.y - a.y * b.x;
}
double dot(Point a, Point b) {
    return a.x * b.x + a.y * b.y;
}

求两条直线交点

判断线段是否相交

对于线段CD来说，判断AB是否在其两侧的方法就很简单了。如果 $\overrightarrow {CA}$ 和 $\overrightarrow{CB}$ 异号就证明AB在CD两侧。（参考叉积的几何意义）

另外对于线段共线（叉积为0）的情况就要特殊判断一下了，具体方法可以在文末参考文献中找到。

一道例题：POJ1066

这里引入一个函数 $Sgn$ :

\operatorname{sgn} x=\left\{\begin{aligned} -1 &: \quad x<0 \\ 0 &: \quad x=0 \\ 1 &: \quad x>0 \end{aligned}\right.

如果两个叉积的积的 $sgn$ 为-1，则一定有交点。为1，则一定不交。如果为0，那么有一定几率在线段端点处交，也可能不交。因为一条线段的端点落在另一条线段上，或者另一条线段的延长线上都会出现0的情况。比如：

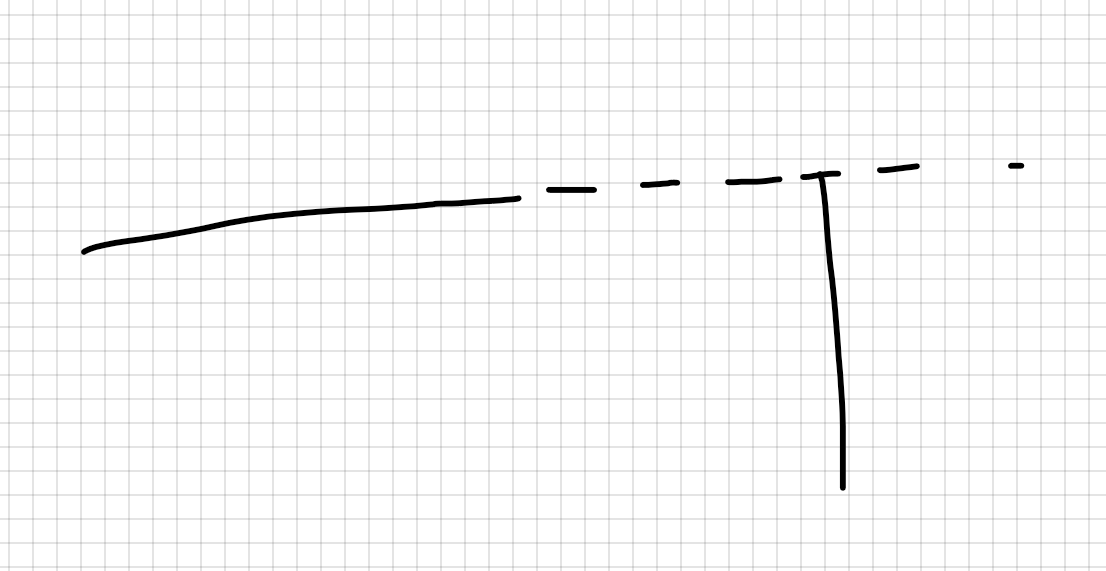
因此我们只需要特判一下即可。

代码（不算端点交）：

算端点交：

判断点和线段相对位置

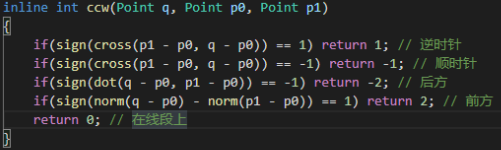
先用叉积判断一下不在线段的延长线上的情况，然后用点积判断在线段前方和后方的情况。（因为点积的几何意义是前一个向量在后一个向量上投影长度和后一个向量长度的积）

另外判断在前方不需要图中的判断模长，只需要把起点终点swap一下即可。

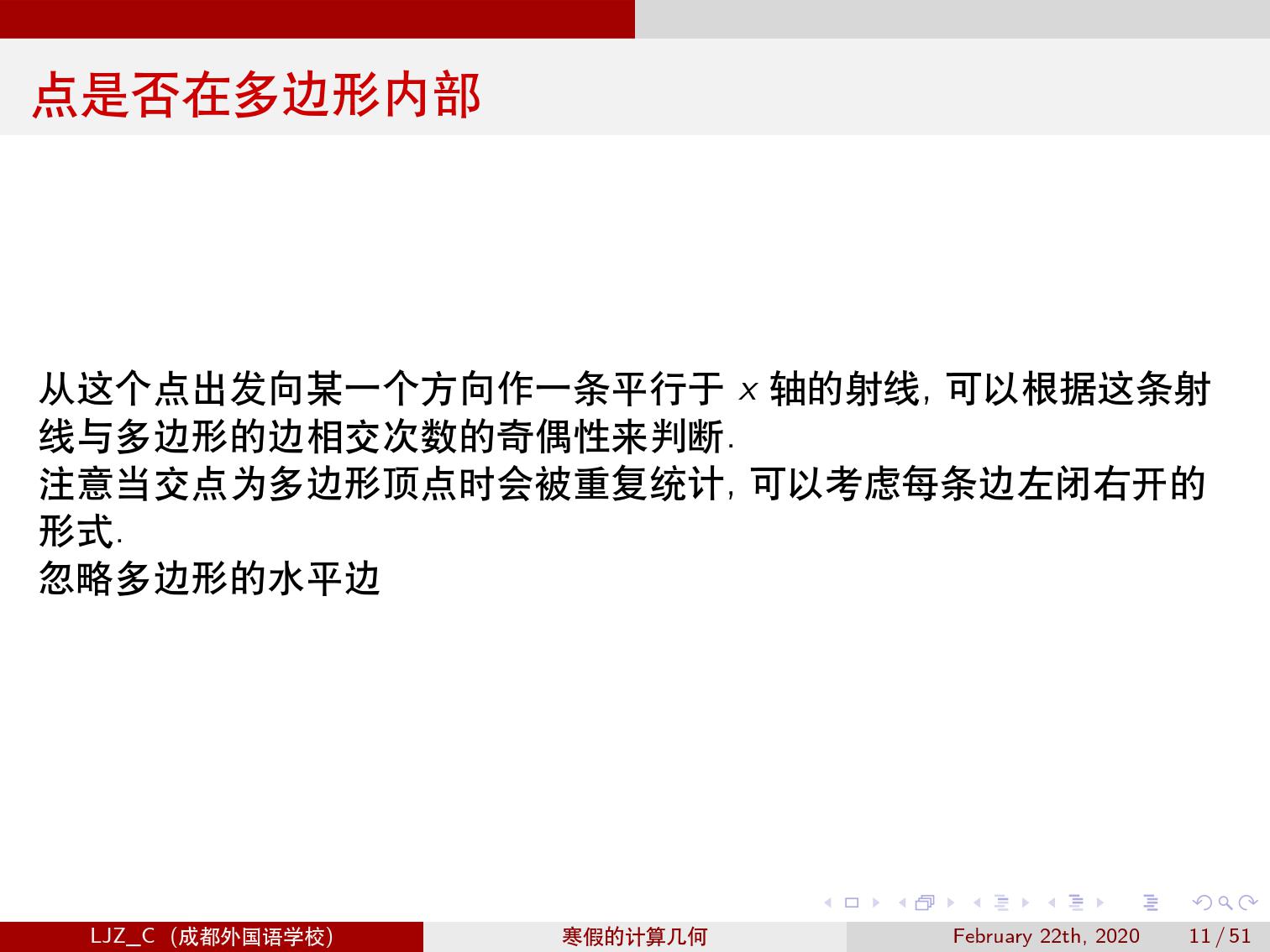
判断点是否在多边形内部

点到直线距离

直线L方程为： $A x+B y+C=0$ ，那么距离为：

\frac{\left|A x_{0}+B y_{0}+C\right|}{\sqrt{A^{2}+B^{2}}}

已知两点求直线一般式方程 $A X+B Y+C=0$ ：

$A=Y 2-Y 1$
$B=X 1-X 2$
$C=X 2 \cdot Y 1-X 1\cdot Y 2$

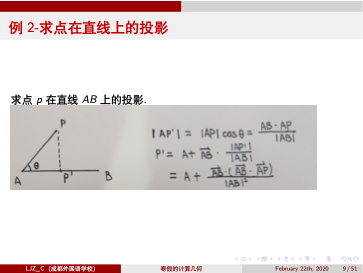
点在直线上的投影

多边形面积

我们有 $\vec{S}_{\triangle P A B}=\frac{1}{2} * \overrightarrow{P A} * \overrightarrow{P B}=\frac{1}{2} *\left(X_{a} Y_{b}-X_{b} Y_{a}\right)$

同时 $S=\sum_{k=1}^{n} \vec{S}_{\triangle P X Y}=\frac{1}{2} * \sum_{k=0}^{n}\left(X_{k} Y_{k+1}-X_{k+1} Y_{k}\right)$

选择一个多边形外的点 $P$ ，然后算 $P$ 和每条边围成的面积。直接用叉积算就好了。

皮克定理

极角排序

极角的定义

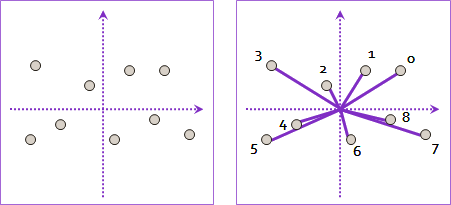
就是按照从X正半轴开始绕着原点逆时针旋转遍历到的顺序进行排序。

d需要注意的一点是，极角的坐标系会常常根据实际应用进行变化。而不是一直平行于平面直角坐标系

实现

向量 $\overrightarrow A$ 排名在 $\overrightarrow B$ 之前 $\Leftrightarrow \overrightarrow A\times \overrightarrow B>0$

证明显然

需要注意的一点是，如果用叉积进行极角排序且所有点不是集中在 $180^\circ$ ，需要将极坐标系分成上下两块（和X轴叉积为正则在上半块）进行分别进行排序。至于为啥，显然。

POJ1696-极角排序板子题

凸包

凸包求解

放在这里了：凸包的处理

稳定凸包

本节转自：POJ 1228 Grandpa's Estate(凸包应用:稳定凸包)

定义

如果一个凸包边界的点正好能确定唯一一个凸包，则称之为稳定凸包

性质

n个凸包边界的点正好能确定唯一一个凸包的 充要条件是 这n个点确定的凸包每条边上至少有3个点。

因为如果当前n个点形成的凸包上,假如有一条边只有两个点,那么你可以添加一个凸包外的点使得该凸包变大,且以前的n个点都还是在凸包的边界上.

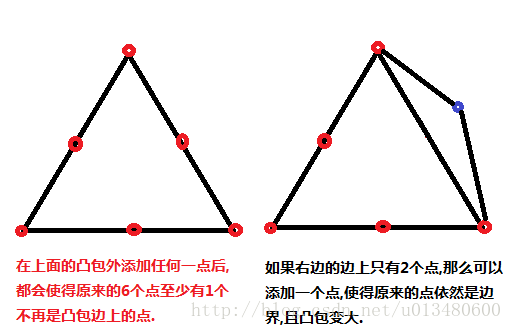
判断凸包稳定性

就利用这个性质根据实际情况自己想办法判断就好了。一些比较细节的问题可以看POJ 1228 Grandpa's Estate(凸包应用:稳定凸包)

半平面交

贴两个板子

S&I算法

复杂度 $n\log n$

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=1000;
const double eps=1e-8;
typedef double db;
struct Point {
    db x,y;
    friend Point operator+(Point a,Point b){return (Point){a.x+b.x,a.y+b.y};}
    friend Point operator-(Point a,Point b){return (Point){a.x-b.x,a.y-b.y};}
    friend Point operator*(Point a,db b){return (Point){a.x*b,a.y*b};}
    friend db operator^(Point a,Point b){return a.x*b.y-a.y*b.x;}
};
struct Line {
    Point a,b;
    db angle;
    Line(){}
    Line(Point vec1,Point vec2){a=vec1,b=vec2,angle=atan2(vec2.y,vec2.x);}
    friend bool operator<(Line a,Line b){return a.angle<b.angle;}
}line[maxn];
Point cross_point(Line l1,Line l2) {
    Point a=l1.a,b=l1.a+l1.b,c=l2.a,d=l2.a+l2.b;
    db rate=((d-c)^(c-a))/((d-c)^(b-a));
    return a+(b-a)*rate;
}
int tot_line;
inline int sgn(db x) {
    if(fabs(x)<eps)return 0;else if(x>0)return 1;else if(x<0)return -1;
}
Line q0[maxn];//deque0 for line, deque1 for cross_point
Point q1[maxn];
int hd=1,tl=1;
void get_convex_hull() {
    q0[hd]=line[1];
    for(int i=2;i<=tot_line;i++) {
        while(hd<tl&&sgn(line[i].b^(q1[tl-1]-line[i].a))==-1)tl--;//test
        while(hd<tl&&sgn(line[i].b^(q1[hd]-line[i].a))==-1)hd++;
        q0[++tl]=line[i];
        if(!sgn(q0[tl].b^q0[tl-1].b)) {
            tl--;
            if(sgn(line[i].b^(q0[tl].a-line[i].a))!=1) {
                q0[tl]=line[i];
            }
        }
        if(hd<tl) {
            q1[tl-1]=cross_point(q0[tl],q0[tl-1]);
        }
    }
    while(hd<tl&&sgn(q0[hd].b^(q1[tl-1]-q0[hd].a))==-1)tl--;//test
    if((tl-hd+1)<3)return;
    q1[tl]=cross_point(q0[tl],q0[hd]);
}
int main() {
    int n;scanf("%d",&n);
    Point tmp[maxn];
    for(int i=1;i<=n;i++) {
        int num;scanf("%d",&num);
        for(int j=1;j<=num;j++)scanf("%lf%lf",&tmp[j].x,&tmp[j].y);
        for(int j=1;j<=num;j++) {
            int p=j-1;if(!p)p=num;
            line[++tot_line]=Line(tmp[p],tmp[j]-tmp[p]);
        }
    }
    sort(line+1,line+1+tot_line);
    get_convex_hull();
    db s=0;
    for(int i=hd;i<=tl;i++) {

        int p=i-1;if(p<hd)p=tl;
        s+=q1[p]^q1[i];
    }
    printf("%.3lf",s/2);
    return 0;
}

朴素算法

复杂度 $n^2$

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long double db;
const int maxn=1000;
const db inf=1e10;
const db eps=1e-17;
int data[maxn][3],cnt1,cnt2=0;
struct Point {
    db x,y;
    friend Point operator+(Point a,Point b){return (Point){a.x+b.x,a.y+b.y};}
    friend Point operator-(Point a,Point b){return (Point){a.x-b.x,a.y-b.y};}
    friend Point operator*(Point a,db b){return (Point){a.x*b,a.y*b};}
    friend db operator^(Point a,Point b){return a.x*b.y-a.y*b.x;}
    Point(){}
    Point(db X,db Y){x=X,y=Y;}
}pt1[maxn],pt2[maxn];
struct Line {
    Point a,b;
    db angle;
    Line(){}
    Line(Point vec1,Point vec2){a=vec1,b=vec2,angle=atan2(vec2.y,vec2.x);}
    friend bool operator<(Line a,Line b){return a.angle<b.angle;}
};
inline int sgn(db x){if(fabs(x)<eps)return 0;if(x>0)return 1;return -1;}
Point cross_point(Point s,Point t,db a,db b,db c) {
    double u=fabs(a*s.x+b*s.y+c);
    double v=fabs(a*t.x+b*t.y+c);
    Point an;
    an.x=(s.x*v+t.x*u)/(u+v);an.y=(s.y*v+t.y*u)/(u+v);
    return an;
}
int n;
db get_s(int cnt) {
    db ans=0;
    for(int i=1;i<=cnt;i++) {
        int p=i-1;if(!p)p=cnt;
        ans+=pt1[p]^pt1[i];
    }
    return ans/2;
}
int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d%d%d",&data[i][0],&data[i][1],&data[i][2]);
    for(int i=1;i<=n;i++) {//枚举获胜者
        pt1[1]=Point(0,0);
        pt1[2]=Point(inf,0);
        pt1[3]=Point(inf,inf);
        pt1[4]=Point(0,inf);
        cnt1=4;
        bool flag=0;
        for(int j=1;j<=n;j++) {
            if(i==j)continue;
            db a=(1.0*data[j][0]-data[i][0])/(1.0*data[j][0]*data[i][0]),b=(1.0*data[j][1]-data[i][1])/(1.0*data[j][1]*data[i][1]),c=(1.0*data[j][2]-data[i][2])/(1.0*data[j][2]*data[i][2]);
            if(!sgn(a)&&!sgn(b)&&sgn(c)>=0){printf("No\n");flag=1;break;}
            cnt2=0;
            for(int k=1;k<=cnt1;k++) {
                if(sgn(a*pt1[k].x+b*pt1[k].y+c)<=0)pt2[++cnt2]=pt1[k];
                else {
                    int p=k-1,ne=k+1;if(!p)p=cnt1;if(ne>cnt1)ne=1;
                    if(sgn(a*pt1[p].x+b*pt1[p].y+c)<0)pt2[++cnt2]=cross_point(pt1[k],pt1[p],a,b,c);
                    if(sgn(a*pt1[ne].x+b*pt1[ne].y+c)<0)pt2[++cnt2]=cross_point(pt1[k],pt1[ne],a,b,c);
                }
            }
            memcpy(pt1,pt2,sizeof(pt2));
            cnt1=cnt2;
        }
        if(flag)continue;
        if(sgn(get_s(cnt1))<=0)printf("No\n");
        else printf("Yes\n");
    }
    return 0;
}

参考文献

LJZ爷爷的课件